Advection-diffusion problems are common in nature. They include mixing of and heat diffusion in fluids.
VelocityCoupling2D
The incompressible Navier-Stokes equations:
$$\partial_t\boldsymbol{u}+(\boldsymbol{u}\cdot\nabla)\boldsymbol{u}=-\frac{1}{\rho_0}\nabla p+\nu\Delta\boldsymbol{u}$$ $$\nabla\cdot\boldsymbol{u} = 0$$
and couple the flow with an advection-diffusion equation (one-way coupling): $$\frac{\partial C}{\partial t}+\boldsymbol{u}\cdot\nabla C=D\nabla^2C$$ For the advection-diffusion equation, the left-hand side describes the advection of C in the presence of an external fluid velocity $\mu$ while the right-hand side contains a diffusion term with diffusion coefficient D.
We use two different lattice descriptors, one for the fluid, and one for the scalar, since they are based on different LBM models:
|
|
And we instantiate two lattices:
|
|
The idea for the coupling is:
Write a data processor which, when applied, receives the two lattices. On every lattice cell, it computes the velocity from the fluid lattice, and copies it to the scalar lattice.
In this example: two lattices, the operation to be performed is not reductive. The base data process functional class is the BoxProcessingFunctional2D_LL
Declaration of the data processor:
|
|
Implementation of clone function:
All Palabos processing functions have a clone function, which creates an exact copy of a class instantiation:
|
|
Implementation of getTypeOfModification:
A data processor must also implement getTypeOfModification :
|
|
The modified argument indicates, for every block, which kind of cell content was modified and needs to be updated. The values it can adopt are the following:
| Argument | Descriptions |
|---|---|
| nothing | No modification |
| staticVariables | Static cell content (e.g. populations) |
| dynamicVariables | Content of dynamics objects (e.g. relaxation time) |
| allVariables | Both static and dynamic content |
| dataStructure | Recreate dynamics object and copy static data |
Implementation of process:
The process method is the actual algorithm.
It is applied repeatedly to rectangular areas on which atomic-blocks of the two fields intersect.
When calling the process method, Palabos provides a domain argument: the coordinates of the domain on which the data processor is executed.

The coordinates of the domain are always local to the atomic-block which is passed first as an argument of the process function. Suppose that atomic-block fluid is passed first and atomic-block scalar is passed second. Suppose also that we have a point (iX, iY), in the local coordinates of fluid, with:
|
|
then the coordinates of the same point local to the block scalar will be (iX+offset.x, iY+offset.y), with:
|
|
To access absolute coordinates, we need to add an offset:
|
|
The Palabos code for the implementation of process:
|
|
The result of coupled cavity2d is displayed:
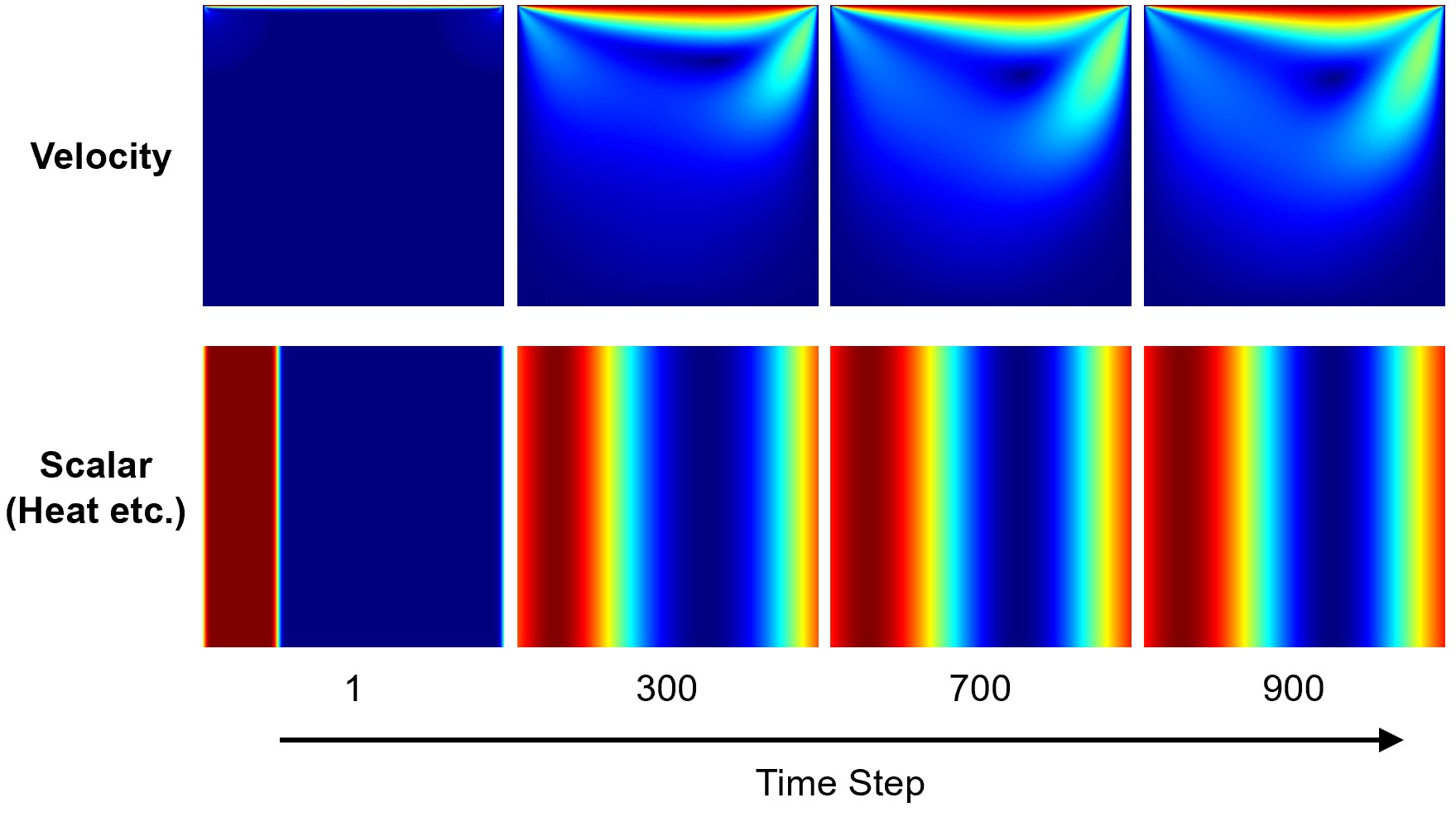
Scalar Field Less Diffusive
The diffusion coefficient D in the BGK model is given by the relaxation time \tau_g, similarity to the viscosity in the NSE: $$ \begin{align*} D={c_s}^2(\tau_g-\frac{\Delta t}{2}) \end{align*} $$ Therefore, to make field less diffusive, them it is need do reduce *D*, which is to reduce \tau_g or increase \omega.
|
|
ApplyProcessingFunctional
Instead of integrating VelocityCoupling2D into ad_lattice, call it manually at every iteration through the function applyProcessingFunctional.
Rules of data processing functionals
- A data processor acts on a subdomain of all atomic-blocks passed to it.
- The data processor can write into that subdomain.
- The data processor can read outside that subdomain, only to an extend given by the communication envelope of the corresponding atomic-block.
- The operation performed by the data processor can be space dependent, if this dependence is formulated in terms of absolute coordinates.
- A data processor must always be written in such a way that executing it on a given domain has the same effect as splitting the domain into subdomains, and then executing it consecutively on each of these subdomains.
Applying and integrating data processing functional
Two ways of using a data processor:
- Execute the processor only once.
- Add the processor to a block and assign to it the role of an internal data processor. The internal data processor can be executed as many times as wished.
To apply the data processor only once, use applyProcessingFunctional:
|
|
To add a data processor to a specific multi-block, one must integrate the processor, by using the function integrateProcessingFunctional:
|
|
In this example, the codes:
|
|
This way, the processor is added to the multi-block lattice and is executed at processor level .
All internal processor added to a multi-block can be executed at any time by a call to the specific block's method executedInternalProcessors, for a specific processor level.
In a multi-block lattice, internal processors have a special role, since the method executedInternalProcessors is automatically invoked at the end of the method collideAndStream after the streaming step.
For this task, the code for ApplyProcessingFunctional:
|
|
Data Processor
Execution order of data processors
- All processor levels are transverse in increasing order starting from level 0.
- Inside a processor level, the data processors are executed in the order they were added to the block.
- Communication (update of envelopes) is performed after an execution of a data processor with write access only when switching from one processor level to the next.
- The processor level can have a negative value. The negative processor level is not executed by the default function
executeInternalProcessors(), which executes all non-negatives levels, but must independently executed by a call to the functionexecuteInternalProcessor(plint level).
Reductive data processors: computing an average
Compute the average value of the N cells in a scalar field C: $$C_{av}=\frac{1}{N}\sum_iC_i$$ The Palabos function to compute this average is the following:
template<typename T>
T computeAverage(MultiScalarField3D<T>& scalarField, Box3D domain)
{
BoxScalarSumFunctional3D<T> functional;
applyProcessingFuncational(funcational, domain, scalarField);
reture funcational.getSumScalar() / (T) domain.nCells();
}
It uses the reductive data processor BoxScalarSumFuncional3D.
Declaration of BoxScalarSumFunctional3D
|
|
BoxScalarSumFunctional3D::process
|
|
BoxScalarSumFunctional3D
|
|
|
|
Boundary Condition for the Scalar Field
see Palabos example BoussinesqThermal2D
GIF Animations
Using gifsicle to generate an animation of GIFs
|
|
Full Codes
|
|